
Das folgende Skript stammt von der Seite
www.PilotUndRecht.de,
die Seite vom Verfasser des Buches
Luftrecht und Flugfunk
Einige Formeln für die
Luftfahrt und andere wichtige Dinge
unter besonderer Berücksichtigung der
CVFR-Berechtigung
Das Nachstehende soll lediglich zur Wiederholung
und Erinnerung dienen – etwa kurz vor der theoretischen
oder praktischen Prüfung. Die Lektüre genügt nicht (!)
zum Erlernen der jeweiligen Thematik.
Anfänger sollten sich nicht abschrecken lassen.
Vieles kann man ohne weitere Erklärung nicht verstehen.
Aber das lernt man alles mit der Zeit.
Inhaltsverzeichnis
Umrechnungen
- Km - NM
- Kts - Km
- m – ft
- m/s – ft/min
- °C - °F
Stationsan-/-abflüge
- Luvwinkel berechnen, um beim Anflug auf eine
Station auf den Soll-Radial zurückzukommen
- Vorhaltewinkel zur Einhaltung des Sollkurses
nach Rückkehr auf den vorgegebenen Radial
- Stationsüberflug
Entfernungen zur Station
- 90°-Methode
- 30°-Methode
- 45°-Methode
- Berechnung der räumlichen Entfernung
Flugbetrieb
- Reichweite eines VOR
- Querneigung beim Standardkreises ermitteln
- Die 1-to-60-Regel
- Abweichungen des Kurskreisels
- Transpondereinstellungen
- Sinkflug einleiten
- (Seiten-)Wind beim Landeanflug
Wetter usw.
- Fahrtmesser
- Startstreckenerhöhung
- Bestimmung der Wolkenuntergrenze
- Bestimmung der relativen Luftfeuchtigkeit aus dem Spread oder umgekehrt
- Barometrische Höhenstufe
- Dichtehöhe
Segelflug
- Schleppgeschwindigkeit
- Kompaßdrehfehler kompensieren
- Beschleunigungsfehler des Magnetkompasses
- Halbkreisflugregeln
- Vom Hoch ins Tief
- Vom Warm ins Kalt
- Vom wahren zum falschen Kurs
- QDM = MH + RB
- Hear more – stear more
- Höhe
- Funkverkehr mit Bodenstellen
- Sonstiges
Die Nautische Meile (NM) ist der 60te Teil (eine Bogenminute)
des Abstands zweier Meridiane am Äquator. Da dieser Abstand 111,11 km
beträgt entspricht die NM 1,852 km.
| |
Km in NM umrechnen |
NM in Km umrechnen |
| Faustformel: |
Km : 2 + 10% = NM |
NM * 2 – 10% = Km |
| Beispiel: |
3 Km : 2 = 1,5
1,5 + 0,15 = 1,65 NM |
3 NM * 2 = 6
6 – 0,6 = 5,4 Km |
... zurück zum Seitenanfang
Entspricht der Formel für Umrechnung Km - NM
| |
km/h in Knoten
umrechnen |
Knoten in km/h
umrechnen |
| Faustformel: |
Km/h : 2 + 10% = kts |
kts * 2 – 10% = Km/h |
| Beispiel: |
140 Km/h : 2 = 70
70 + 7 = 77 kts |
65 kts * 2 = 130
130 – 13 = 117 Km/h |
... zurück zum Seitenanfang
| |
Meter in Fuß umrechnen |
Fuß in Meter umrechnen |
| Faustformel: |
m * 3 + 10% = ft |
ft : 3 – 10% = m |
| Beispiel: |
1.000 m * 3 = 3000
3000 + 300 = 3.300 ft |
1.000 ft : 3 = 333
333 – 33,3 = 300 m |
oder
| |
Meter in Fuß umrechnen |
Fuß in Meter umrechnen |
| Faustformel: |
m / 3 * 10 = ft |
ft / 10 * 3 = m |
| Beispiel: |
1.000 m * 3 = 330
330 * 10 = 3.300 ft |
1.000 ft / 10 = 100
100 * 3 = 300 m |
... zurück zum Seitenanfang
| |
m/s in Ft/min
umrechnen |
Ft/min in m/s
umrechnen |
| Faustformel: |
m/s * 200 = ft/min |
ft/min : 200 = m/s |
| Beispiel: |
3 m/s = 600 ft/min |
1000 ft/min = 5 m/s |
... zurück zum Seitenanfang
Die Fahrenheit-Skala wird überwiegend im angelsächsischen
Sprachraum verwandt. Dort hergestellte Temperaturmesser
sind mit dieser Skala geeicht. Nähere Informationen und
einen Online-Umrechner finden Sie
hier
| |
°F in °C
umrechnen |
°C in °F
umrechnen |
| Formel: |
°C = 5/9 * (°F – 32°) |
°F = (9/5 * °C) + 32° |
| Beispiel: |
68° Fahrenheit sind
5/9 * (68 °F – 32°) =
5/9 * 36 = 20 °Celsius |
35° Celsius sind
(9/5 * 35 °C) + 32 =
(9 * 7) + 32 = 94 °Fahrenheit |
... zurück zum Seitenanfang
Dem Flugzeugführer wird vorgegeben, ein Funkfeuer auf dem
Radial 160 anzufliegen. Er ermittelt, daß die Dauer des
Fluges zur Station 12 Minuten sein wird. Nach 4 Minuten
befindet sich das Flugzeug auf Radial 155. Um wieviel Grad
muß er den Luvwinkel korrigieren?
| Faustformel: |
Verhältnis aus Restflugzeit und Versetzungsdauer mal Peilsprung |
| Genauer: |
WCA = Restzeit zur Station (min) / Dauer der Versetzung (min) * Peilsprung |
| Beispiel (s.o.): |
8 / 4 * 5 = 10° |
| Ergebnis: |
Da der Wind offensichtlich von links kommt (kleineres Radial!),
muß das Heading somit um 10° reduziert werden. |
... zurück zum Seitenanfang
Kehrt man beim Anfliegen einer Station bzw. beim Abfliegen von
einer Station nach Feststellen eines Peilsprungs auf den ursprünglichen
Sollkurs zurück, dann ist der Luvwinkel nach folgenden Faustregeln
zu ermitteln:
-
eineinhalbfacher Peilsprung, wenn die Zeit der Versetzung
kürzer als die Hälfte (etwa ein Drittel) der Gesamtzeit zur Station
beträgt.
-
einfacher Peilsprung bei etwa halber Flugzeit.
-
halber Peilsprung, wenn nur noch etwa ein Drittel
der Gesamtflugzeit zum Peiler benötigt wird.
Ein
Stationsüberflug (NDB oder VOR) geschieht in folgenden Schritten:
- Kommt man in die cone of silence oder cone
of confusion, so wartet man einen Moment und
dreht dann mit einer Standardkurve auf den
neuen Kurs.
- Liegt der neue Kurs an, so wird die Stopuhr
gedrückt.
- Jetzt fliegt man 30 sek. lang den neuen Kurs
und stellt während dieser Zeit das neue
(outbound-)Radial ein. Man fliegt also
30 sek. parallel zum eingestellten
Radial.
- Dann schneidet man das eingestellte Radial
mit 30° an.
Beispiel:
- Anflug auf die Station mit 360° (auf
Radial 180)
- Überflug und Eindrehen auf Kurs 45°
- Drücken der Stopuhr und Fliegen mit
45° (parallel zum R045)
- Einstellen R045 auf VOR. 30 Sekunden lang
Kurs 75° fliegen bis Radial 045
erreicht ist. Kurz vorher erneut 45°-Kurs
eindrehen.
Der Überflug über ein NDB erfolgt im
Prinzip gleich, nur das hier nicht R045,
sondern das Interception-Heading (im Beispiel
als 75°) eingedreht werde muß
-
Zunächst Kompaßkurs so ändern, daß ein RB von 80°
oder 100° bzw. 260° oder 280° angezeigt wird.
-
Dann Kurs und Geschwindigkeit beibehalten, bis
sich RB auf 85°, 95° bzw. 265°, 275° ändert
-
Zeit nehmen bis RB auf 95°, 85° bzw. 275°, 265°
steht.
-
Formel anwenden: Abstand zur Station in Min = gestoppte Zeit
(sek) / Peilsprung
Beispiel:
Kurs ist 50° (MH). Angezeigtes RB ist 345°. Flugzeug dreht (nach rechts) vom Kurs
ab, bis RB von 280° angezeigt wird. Kurs und Geschwindigkeit (bspw. 140 km/h)
halten bis Radiokompaß RB 275° zeigt. Jetzt Zeit bis zum Erreichen des RB 265°
nehmen (in Sekunden). Beispiel: 150 Sekunden.
Ergebnis: Flugzeug ist (150 / 10 =) 15 Minuten von der Station entfernt.
ggf. Entfernungszeit umrechnen in Entfernungsstrecke
Im Beispiel beträgt die Entfernung also 35 km (wenn v = 140 km/h).
... zurück zum Seitenanfang
-
Stehende Peilung erfliegen
-
Steuerkurs um 30° nach links oder recht ändern (beim ADF werden
logischerweise immer 30° oder 330° Relative Bearing angezeigt)
-
Nach Ausleiten der Kurve auf neuem Kurs Zeit nehmen
-
Mit gleichem Kurs und gleichbleibender
Geschwindigkeit weiterfliegen
-
Zeit nehmen, wenn Peilung mindestens ±5°
(empfohlen ±10°) weiter gewandert ist.
-
Formel anwenden: Abstand zur Station (min) = gestoppte Zeit (sek) / 2 * Peilsprung
120 Sekunden Flugzeit für einen Peilsprung von 10° ergibt [120 / (2 * 10) =] 6 Minuten.
Daraus folgt bei 150 km/h eine Entfernung zur Station von 15 Km.
... zurück zum Seitenanfang
Beruht auf der Tatsache, daß in einem Dreieck die beiden
Katheden gleich lang sind, wenn zwei Winkel 45° betragen.
- Radial ±135° vom Kurs eindrehen (also bspw. bei
Nordkurs R135 oder R225, vgl. Bild). Liegt die Station rechts der Kurslinie
–225°, links der Kurslinie +135°
- Zeit nehmen, sobald Flugzeug auf diesem Radial ist
(Nadel des VOR-Anzeigers steht in der Mitte)
- Radial um ±45° verändern (bei Nordkurs also R090
oder R270 einstellen, vgl. Bild). Liegt die Station rechts der Kurslinie +45°,
links der Kurslinie -45°
- Kurs und Geschwindigkeit beibehalten
- Erneut Zeit nehmen wenn neu eingestelltes Radial erreicht ist

Zeitdifferenz entspricht der Entfernung zur Station.
Hat man 90 Sekunden bei 150 km/h gestoppt, so ist man 90 Sekunden, also 3,75 km
von der Station entfernt.
Beispiel:
mwK ist 325°. Station liegt links voraus. Einzustellen
ist (325° + 135° = 460° = ) R100. Beim Überflug des Radials wird die Stopuhr
eingestellt und danach ein um 45° kleineres Radial eingestellt, also Radial 55.
Sobald dieses Radial erreicht wird, kennt man die (zeitmäßige) Entfernung zur
Station.
Die 45°-Methode ist sehr umständlich beschrieben.
Besser ist es, man überlegt sich zunächst, welchen Radial man mit seiner
Kurslinie senkrecht schneiden wird. Fliegt man mit 330° nördlich an der Station
vorbei, so wäre das R060. Dann überlegt man sich, welche Radiale man vorher
überfliegt. Dazu erhöht man R060 um 45° und erhält also R105°.
Nachdem man die Flugzeit zu einer Station mit der 30°-, 45°- oder
90°-Methode errechnet hat, kann man die Entfernung aus der Fluggeschwindigkeit
TAS und der festgestellten Flugzeit ermitteln:
Entfernung (NM) = Geschwindigkeit (kt) * Zeit (Minuten) / 60
Folgende Eckdaten sollte man im Kopf haben:
Bei TAS=60 kt legt man 1 NM pro Minute zurück, bei 120 kt
sind es 2 NM pro Minute, bei 90 kt 1,5 NM usw.
Ist das Flugzeug mit einem
DME (Distance measuring
equipment) ausgestattet, so kann die
Entfernung zu einem voreingestellten VOR/DME
vom DME angezeigt werden.
Reichweiten bis zu 200 NM sind möglich.
Reichweite (in NM) = 1,25 * √Flughöhe (ft)
Beispiel: Bei einer Flughöhe 2025 ft beträgt die Reichweite
des VOR (1,25 * 45 =) 56,25 NM.
Bei einem Standardkreis beträgt die Drehgeschwindigkeit
3° pro Sekunde. Das heißt, ein Vollkreis (360°) dauert genau
2 Minuten, eine 90°-Kurve dauert 30 Sekunden usw.
Die Faustformel zur Ermittlung der Querneigung, die das
Flugzeug für den Flug eines Standardkreises einnehmen muß,
lautet:
TAS(kn) : 10 + 7
Beispiel: Geschwindigkeit ist 100 kn. Querneigung des Standardkreises ist gesucht:
100 kn : 10 + 7 = 17°
Die Querneigung muß also 17° betragen.
Anmerkung: Wichtig ist, daß man die richtige Maßeinheit
(Knoten) kennt. Die entsprechende Frage in der Prüfung
stellt genau darauf ab. Daß Punktrechnung vor Strichrechnung
geht, sollte keiner gesonderten Betonung bedürfen.
ermittelt einen Abweichungswinkel und basiert auf dem Umstand,
daß der Tangens von α ungefähr α /60 beträgt, jedenfalls
solange α kleiner als 15° ist. Auch der Sinus von α
ist α/60, solange α kleiner als 35° ist.
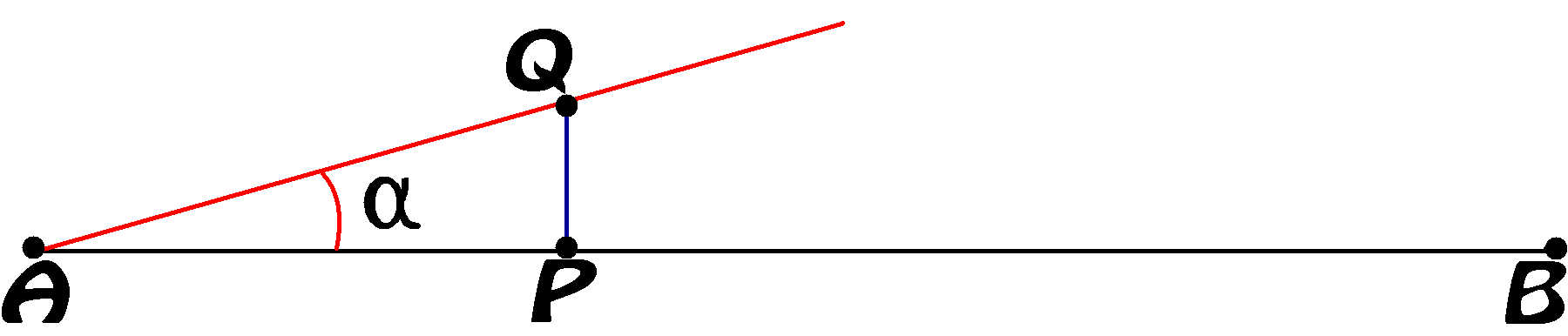
Gewollte Kursstrecke ist A – B.
Tatsächlich geflogener Kurs ist A – Q.
Das Dreieck A-P-Q ist rechtwinklig.
Winkel α
kann man mit Hilfe der Formel
tan(α) = Gegenkathede durch Ankathede
ermitteln. Ersetzt man
tan(α)
durch α/60, so erhält man die Formel
α / 60 = Gegenkathede / Ankathede | auf beiden Seiten multipliziert mit 60 ergibt:
α = Gegenkathede / Ankathede * 60 | oder für die Berechnung der Korrekturwinkels
α = 60 * Querablage / Teilstrecke
Beispiel:
Auf einer 80 Km langen Strecke merkt der Pilot querab von Punkt P, daß er statt
bei Punkt P bei Punkt Q angekommen ist. Er ermittelt die Abweichung (P-Q) auf
der Karte mit 5 Km und die Strecke A-P mit 30 Km. Eingesetzt in die vorgenannte
Formel ergibt sich:
α
1; = 60 * 5 / 30 = 10°
Korrigiert der Pilot also um 10°, so fliegt er einen Kurs, der parallel zum geplanten Kurs
verläuft. Will er unmittelbar Punkt B anfliegen, so muß er auch noch den Winkel
β berechnen. Hier gilt Entsprechendes:

α
2 = 60 * Querablage /
Reststrecke
hier also: α = 60 * 5 /
50 = 6
Lösung der Aufgabe:
Um direkt das Ziel (B) anzufliegen, müßte der
Pilot also um (10° + 6° =) 16°
korrigieren.
errechnet man mit der Formel
[15° x sin(geographische Breite)] pro Stunde
Erklärung:
Ein schnell rotierender Kreisel will seine Lage im Raum beibehalten. Da die Kreiselachse
des Kurskreisels parallel zur Erdoberfläche ausgerichtet ist, entsteht eine
immer größer werdende Abweichung, wenn sich der Kreisel mit der Erde drehen
muß. Eigentlich wandert also nicht die Kreiselachse, sondern das Bezugssystem
Erdoberfläche.
Die Größe der scheinbaren Wanderung (Drift) hängt ab von der geographischen Breite.
Am Äquator ist sie Null, an den Polen beträgt sie 15° pro Stunde. In unseren
mittleren Breiten wandert der der Kurskreisel alle 15 Minuten um 3° und muss
daher in Abständen von etwa 15 Minuten nach dem Magnetkompass nachgestellt
werden.
Beispiel:
Bei einem auf dem Flugplatz Butzbach stehenden Flugzeug ist der eingeschaltete
Kurskreisel genau auf Norden eingestellt. Welche Abweichung würde er nach zwei
Stunden aufweisen?
2 x 15° x sin(50° 20' 40'') =
30° x sin(50,4°) =
30° x 0,77 =
23°
Das scheinbare Wandern des Kurskreisels muß von seiner wahren Drift unterschieden
werden. Sie beruht auf mechanischen Umständen (Kreiselunwucht, mechanische Fehler,
Herstellungstoleranzen, Bewegungen des Flugzeugs).
| Situation |
Transpondereinstellung |
| Grundsätzlich |
7.000 |
| früher: |
In älteren Büchern liest man noch
Unter 5.000 Fuß : 0021 (empfohlen)
Über 5.000 Fuß : 0022 (vorgeschrieben)
Beides gilt seit dem Jahr 2007 nicht mehr! |
|
|
| Highjacking |
7500 (Eselsbrücke: sieben-fünf = Entführung
oder auch seven five, man with knife) |
| Funkausfall |
7600 (Eselsbrücke: seven six, hörst nix) |
| Notfall |
7700 (Eselsbrücke: seven seven: next to heaven |
Für die zweite Eselsbrücke zur 7500 danke ich Fliegerfreund Ulrich Weber, Donzdorf, für die Eselsbrücken zu 7600 und 7700 ein Dankeschön an den Fliegerfreund Peter Breuer, München
... zurück zum Seitenanfang
Wer nach einem Überlandflug (viel) zu früh mit dem Sinken beginnt,
kommt weit ab von der Platzrunde auf Platzrundenhöhe an und fliegt
dann i.d.R. deutlich unterhalb der Überlandflughöhe zum Platz. Wer
hingegen zu spät mit dem Sinken anfängt, muss zu steil sinken, was
auf die Ohren (der Mitflieger) gehen könnte.
Es ist deshalb sinnvoll, den Landeanflug so einzuleiten, dass man
am Ende des Absteigens in Platzrundenhöhe in die Platzrunde
einfliegen kann.
Wer bei V
G von 90 Kn mit 500 Fuß/Min (entspricht 2,5 m/sec)
sinkt, kann sich einer Faustformel bedienen:
Entfernung (in NM) = Höhe über Platzrunde (in Fuß) : 1000 * 3
Wer (bei gleicher Sinkrate) mit geringerer V
G sinkt, muss
pro 10 Kn Unterschied zwei NM abziehen (und umgekehrt).
Beispiel
Aktuelle Höhe: 8.000 Fuß,
Platzrunde Zielflugplatz: 2.000 Fuß
V
G: 70 Kn
Entfernung = 6.000 : 1000 * 3 =
18 NM
Korrigiert um 20 Knoten geringere V
G während des Sinkfluges,
also 2 mal 2 NM subtrahieren. Ergebnis: Der Sinflug muss in 14 NM
begonnen werden.
Wir alle kennen Dialoge folgener Art:
| Pilot: |
"Endanflug Piste zwo fünf." |
| Boden: |
"Piste frei; Wind zwo acht null Grad mit eins fünf Knoten." |
| Pilot:° |
"Verstanden." |
Aber mal ehrlich: Wer hat schon einmal aus einer solchen Windangabe
etwas Sinnvolles abgeleitet. Tatsächlich fliegen wir Privatflieger
doch meistens nach Gefühl, bestenfalls werfen wir noch einen Blick auf
den Windsack. Wer will auch in den schwierigsten Momenten, die die
Fligerei zu bieten hat, noch großartig rechnen (für das obige Beispiel):
cos(300 minus 250) * 15.
Einfacher geht es mit einer kleinen Tabelle, die sich aus folgender
Feststellung ergibt: Weicht die Windrichtung von der Landerichtung
mehr als 15° ab, nimmt man eine Seitenwindkomponente von 25% der
Windgeschwindigkeit an usw.
| Winkel |
% V(Wind) |
| 15° |
25% |
| 30° |
50% |
| 45° |
75% |
| ≥ 60° |
100% |
Die so geschätzten Seitenwindkomponenten sind zwar leicht höher als bei präziser
Berechnung, doch ist der Pilot mit ihnen auf der sicheren Seite. Zwischenwerte
können interpoliert werden.
Beispiel (aus dem obigen Dialog): Der Winkel zwischen Landerichtung und
Windrichtung beträgt 30°. Die Seitenwindkomponente beträgt damit 7,5 Knoten (50% von 15).
Mit zunehmender Flughöhe zeigt der Fahrtmesser
zu kleine Eigengeschwindigkeiten an, m.a.W. die
Eigengeschwindigkeit (TAS) ist höher als die
angezeigte Geschwindigkeit (IAS). Grund: Mit
der in der Höhe abnehmenden Luftdichte wird
auch der Staudruck geringer.
(Faustformel:) Deshalb erfolgt je 1.000 ft Flughöhe ein Zuschlag von 2% zur IAS.
Beispiel: IAS = 110 kt, Flughöhe 3.000 ft, TAS = 110 + (2,2 * 3) = 116,6 kt.
Die benötigte Startstrecke (Strecke bis zum Erreichen von 15 m Höhe) hängt
stark von der Temperatur, der Platzhöhe und -beschaffenheit ab. Lesen Sie
unbedingt auch die Ausführungen zur
Dichtehöhe.
Allgemein kann man folgende Faustregeln anwenden:
Die Startstrecke erhöht sich:
- pro 100 m (300 ft) Platzhöhe über NN um 2,5%
- (ab 15° C:) pro 1° C mehr Temperatur um 1%
- pro 1% Steigung um 10%
Bsp.: Für den Falken SF 25 C (Bj.: 1978) beträgt die Startstrecke laut Handbuch bei
einer Platzhöhe von 0 m und 0° Außenlufttemperatur 330 m. Gestartet werden soll
von Bad Berka (Platzhöhe: 305 m; Steigung der Betriebspiste zwo fünf: 2%;
Temperatur 22° C). Berechnung der Startstrecke:
| Startstrecke nach Flughandbuch (0 ft MSL, Piste eben, Temp 0° C): |
330,00 m |
| Für die Platzhöhe sind 7,5% von 330 m = 24,75 m anzusetzen: |
25,00 m |
| Zusammen: |
355,00 m |
| Für die Steigung der Piste 20% von 355 m: |
71,00 m |
| Für die Temperatur 7% von 426 m: |
30,00 m |
| tatsächlich benötigte Startstrecke: |
456,00 m |
Spread (deutsch: Spreizung) ist die Differenz
zwischen aktueller Temperatur und Taupunkt,
also der Temperatur, bei der eine Luftfeuchtigkeit
von 100% erreicht wäre. Bei einer aktuellen Temperatur
von 11° und einem Taupunkt von 7° ist der Spread also 4.
Sinkt die Temperatur um 4° oder mehr, kommt es zur
Kondensation des in der Luft enthaltenen Wassers
(Nebel- oder Wolkenbildung).
Kennt man den Spread, kann man die Wolkenuntergrenze
nach folgender Faustformel bestimmen:
Wolkenuntergrenze (in Fuß) = Spread * 400 Fuß
oder
Wolkenuntergrenze (in m) = Spread * 122 m
Beispiel:
Lufttemperatur 25° C; Taupunkt 15° => Spread = 10
Wolkenuntergrenze = 10 * 400 Fuß = 4.000 Fuß
Bis zu einem Spread (hierzu siehe
Bestimmung der Wolkenuntergrenze)
von 10° gilt folgende Faustformel: Pro Grad Spread zieht man 5%
von 100% Luftfeuchtigkeit ab und erhält die relative Luftfeuchtigkeit.
Bsp.: Spread ist 7°. 100 – 7 * 5 = 65. Rel. Luftfeuchte also 65%
Umgekehrt liegt bei einer relativen Luftfeuchte von bspw. 85% der Spread nur bei 3°.
... zurück zum Seitenanfang
gibt an, wie viele Meter man steigen (oder sinken) muß, um einen Druckunterschied
von 1 hPa feststellen zu können.
Die barometrische Höhenstufe beträgt:
| In NN |
8 m/hPa |
| In 2.000 m MSL |
10 m/hPa |
| In 4.000 m MSL |
12,5 m/hPa |
| In 6.000 m MSL |
15,5 m/hPa |
Als Faustformel kann man bis zu einer Höhe von 6.000 m MSL annehmen:
Höhenstufe = 8 + Höhe in Km MSL
Bsp.: in 5.000 m über MSL (= 5 km MSL) beträgt die Höhenstufe 8 + 5 = 13 m/hPa.
Jeder weiß, dass die Steigkraft eines Lfz. mit zunehmender Höhe geringer
wird. Die Luft wird "dünner", was insbesondere drei Konsequenzen nach
sich zieht. (1) das Flugzeug wird nicht mehr so gut "getragen"
(weniger Auftrieb). (2) der Propeller verliert an Wirkungskraft (weniger
Vortrieb) und (3) das Triebwerk muss mit weniger Sauerstoff auskommen.
Die Dichte der aktuellen Luft(schicht) hängt aber nicht allein von der Höhe
ab, in der man fliegt oder startet. Auch und vor allem der aktuelle
Luftdruck
und die aktuelle
Temperatur bilden zwei wichtigen Einflussgrößen.
Ist der Luftdruck höher oder die Temperatur kälter, werden wir mit der
ansonsten ausreichenden Startstrecke keine Probleme bekommen. Umgekehrt kann
es aber so sein, dass wir auf diesem Platz mit diesem Flugzeug nicht mehr
starten können. In diesem Fall wäre die aktuelle Dichtehöhe zu hoch.
Das ist die Höhe in der Standardatmosphäre, die der in der Start- oder Flughöhe
des Flugzeugs herrschenden Luftdichte entspricht oder mit andern Worten:
Dichtehöhe ist die temperaturkorrigierte Druckhöhe.
Die Dichtehöhe berechnet man (grob) wie folgt:
Zunächst ermittelt man die Druckhöhe. Das geht am einfachsten, indem man
auf dem Höhenmesser den Luftdruck der Standardatmosphäre (1013,2 hPa)
einstellt. Der Höhenmesser zeigt dann die Druckhöhe an.
Umständlicher ist es, die Druckhöhe zu errechnen. Dazu benötigt man das
QNH. Das kann man ebenfalls ablesen, man muß jetzt nur umgekehrt
vorgehen und im Höhenmesser die Platzhöhe einstellen. Dem Justierfenster
kann man dann das QNH entnehmen. Nun lautet die Formel zur Berechnung
der Druckhöhe (etwa eines Flugplatzes):
Druckhöhe(Platz) = Platzhöhe + (1013 - QNH) * 30
Da das Problem grds. nur eintritt, wenn der aktuelle
Luftdruck niedriger ist, kann davon ausgegangen werden, dass das QNH
stets kleiner ist als 1013 hPa. Der in der Formel benutzte Faktor 30
entspricht einer Barometrischen Höhenstufe.
Ganz genau müsste man stattdessen zwar mit 27 rechnen. Aber für
den Alltag reicht der leichter zu handhabende Faktor 30.
Nun müssen wir zur Ermittlung der
Dichtehöhe noch die Temperatur
berücksichtigen. Und zwar muss man für jedes Grad, um das die aktuelle
Temperatur höher ist als 15° (das ist der Wert der Standardatmosphäre)
120 Fuß addieren. Liegt die aktuelle Temperatur also bei 25°, so
erhöht sich die Druckhöhe um 1.200 Fuß. Die Formel lautet also:
120 * (aktuelle Temp. - 15)
Fasst man die beiden Formeln zusammen, liest sich das wie folgt:
Dichtehöhe(Platz) = Platzhöhe + [(1013 - QNH) * 30] + [120 * (aktuelle Temp. - 15)]
Da das ein bisschen schwer zu merken ist, sollte man sich die Formel
in sein persönliches Flugbuch eintragen.
Beispiel: Bad Berka (Elev. 1.042 Fuß), 33 °C, QNH = 998 hPa
Der aktuelle Luftdruck liegt 15 hPa unter Standard, d.h. die Druckhöhe
ist (15 * 30) 450 Fuß höher als die Platzhöhe (312 m). Die Druckhöhe
beträgt also in Bad Berka aktuell (1042 + 450) = 1.492 Fuß.
Addiert man die Temparatureinwirkung (18 * 120) = 2.160 Fuß erhält
man eine Dichtehöhe von
3.652 Fuß. Die Dichtehöhe ist also
mehr als drei mal so hoch, wie die wirkliche Höhe des Platzes.
Wie einleitend erwähnt, ist das nur die
grobe Berechnung der
Dichtehöhe. Weil ein Besucher meiner Homepage mich - zutreffend -
darauf aufmerksam gemacht hat, dass die Formel noch einen Fehler enthält,
möchte ich diesen auch nicht vorenthalten (vielen Dank an Martin H.).
Der Fehler liegt darin, dass die Temperatur nicht höhenbereinigt ist.
Der Formelteil
120 * (aktuelle Temp. - 15)
stimmt ja nur in Meereshöhe (MSL). Genaugenommen muss man diesen Teil
wie folgt korrigieren.
120 * (aktuelle Temp. - [15 - Elevation * 2°C / 1000ft])
Im Beispiel für Bad Berka (s.o.) wäre also
Dichtehöhe = 1042 (elevation) + 450 (Druckkorrektur) + 120 * [33 - (15 - 1042 * 2 / 1000)]
Dichtehöhe = 1042 + 450 + 120 * [33 - (15 - 2)]
Dichtehöhe = 1042 + 450 + 2400
Dichtehöhe = 3892 Fuß
Die Dichtehöhe läge damit noch um weitere 240 Fuß höher als das oben
genannte grobe Ergebnis ausweist.
Dies veranlasst mich, nochmals auf meinen
Haftungsausschluß hinzuweisen.
Nach einer Faustformel soll die Schleppgeschwindigkeit beim F-Schlepp
im Bereich von
Vmin = VSO x 1,2
bis
Vmax = VSO x 1,5
des Schleppflugzeuges liegen. Der F-Schlepp ist also im konkreten Fall
nur möglich, wenn das geschleppte Lfz. in diesem Bereich flugfähig ist.
Beispiel: Bei einer Wilga liegt die Überziehgeschwindigkeit
(VSO)
bei 95 km/h.
Der Schlepp sollte sich also im Geschwindigkeitsbereich von
114 km/h und 143 km/h bewegen.
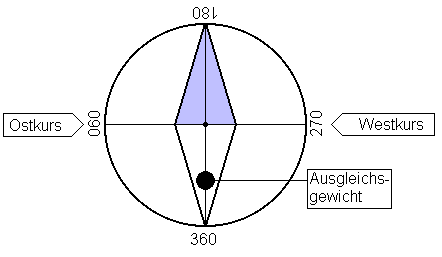
Die Feldlinien des Erdmagnetismus zielen in
unseren Breitengraden mit etwa 65° in den
Erdboden (Inklination). Damit die Nadel des
Magnetkompasses nicht auch auf den Erdboden
zeigt, wird ein kleines Gewicht auf der nach
Süden zeigenden Nadel-Hälfte angebracht. Das
Ungleichgewicht der beiden Nadelteile bewirkt
aber wegen des Gesetzes über die Trägheit der
Masse, daß der Magnetkompaß Drehfehler aufweist,
und zwar bei Veränderungen von Richtung (1.)
und Geschwindigkeit (2.).
Nach N
orden v
orher ausleiten
Nach S
üden
überkurven (später ausleiten)
(oder: Nach
Süden
später)
Beispiele:
- Kurs ist 90°. Neuer Kurs soll Nordkurs sein. Kurve muß ausgeleitet werden bei 30°
- Nordkurs. Rechtskurve auf Südkurs. Ausleiten bei 210°
- Kurs 250°. Gewollter Kurs Südkurs. Ausleiten bei 150°
Will man nicht genau auf Nord (360°) oder Süd (180°) eindrehen, so muß man entsprechend
vorher oder später ausleiten:
Bei 330° bzw. 030°: 20° früher
Bei 300° bzw. 060°: 10° früher
Bei 150° bzw. 210°: 20° später
Bei 120° bzw. 240°: 10° später
Bei Nord-Süd-Kursen haben Änderungen der
Geschwindigkeit keinen Einfluß auf die
Bewegung der Kompaßnadel! Bei Ost-West-Kursen
hingegen schon:
D
Rücken (beschleunigen)
a
Abweichung der Anzeige nach No
Rd.
Z
IEhen (verlangsamen)
a
Abweichung der Anzeige nach S
Üden.
Oder Merkwort
ANDS.
Acceleration =>
Nordabweichung;
Deceleration
=>
Südabweichung.
Beschleunigt man auf Ostkurs (Kompaßanzeige 90°), so wird die Kompaßanzeige kleiner.
Beschleunigt man auf Westkurs (Kompaßanzeige 270°), so wird die Kompaßanzeige größer.
IFR-Flugverkehr findet über 5.000 Fuß/MSL auf
den Flugflächen 60, 70, 80, 90 usw. statt.
Dem VFR-Verkehr sind die dazwischen liegenden
Flugflächen 55, 65, 75, 85, 95 usw. zugewiesen.
Welche von diesen Flugflächen man als VFR-Flieger
zu benutzen hat, richtet sich danach, ob man
eine (mißweisend) westliche oder östliche Richtung
fliegt. Man kann folgende Merkformel verwenden:
Nach
Osten kr
umm,
nach W
esten g
erade
Bei Kursen von 0° bis 179° (mißweisend), müssen die Flugflächen
55,
75,
95 gewählt werden, bei Kursen von 180° bis 359° die Flugflächen
65,
85,
105 usw.
Bsp.: Rechtweisender Kurs ist 178°. Mißweisung 3° West. Kann auf Fl 65 geflogen werden?
Ja, da mißweisender Kurs 181° ist, also Westkurs geflogen wird, muß auf einer
"geraden" Flugfläche geflogen werden.
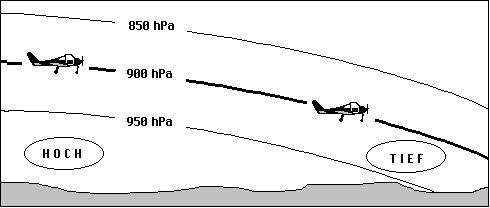
Bringt zum Ausdruck, daß der Höhenmesser zu große Höhen anzeigt,
wenn man von einem Hochdruckgebiet in ein Tiefdruckgebiet fliegt,
ohne den Höhenmesser zwischendurch nachgestellt zu haben (und zwar
auf das QNH des nächstgelegenen Flugplatzes mit Verkehrskontrolle).
Man fliegt also tatsächlich niedriger, als der Höhenmesser anzeigt.
Das liegt – kurz erklärt – daran, daß eine Linie gleichen Luftdrucks,
die zwischen einem Hochdruckgebiet und einem Tiefdruckgebiet liegt,
vom Hochdruck zum Tiefdruck verlaufend sich dem Erdboden nähert. Im
Schaubild zeigt der Höhenmesser beides Mal den gleichen Höhenwert an.
Bei unveränderter Einstellung der Bezugsgröße zeigt der Höhenmesser
auf beiden Positionen des Flugzeugs die gleiche Höhe an. Hielte man
die Höhe nur nach dem Höhenmesser (IFR), prallt man in der obigen
Situation irgendwann auf dem Boden auf.
Faustformel:
Pro hPa muß man mit ca. 30 ft Höhenunterschied rechnen. Fliegt
man also bspw. mit einer Einstellung des Höhenmessers von 1020 hPa,
herrscht aber tatsächlich ein Luftdruck von 993 hPa, so zeigt der
Höhenmesser eine um (27 * 30=) 810 ft bzw.
245 m zu große Höhe an.
... zurück zum Seitenanfang
Bringt zum Ausdruck, daß der Höhenmesser zu hohe Höhen anzeigt, wenn
man in eine Luftmasse einfliegt, deren Temperatur geringer ist als
die Standardtemperatur. Man fliegt also tatsächlich niedriger, als
der Höhenmesser anzeigt. Erklärung: Luft ist ein Gasgemisch. Die
Moleküle eines Gases bewegen sich bei dessen Erwärmung schneller
und erzeugen damit höhere Aufprallkräfte, wodurch zugleich der Druck
erhöht wird. Fliegt man in ein Kaltgebiet, läuft der Vorgang umgekehrt.
Der Druck wird bei tatsächlich gleicher Höhe niedriger, das Flugzeug
steigt scheinbar. Korrigiert man hingegen entsprechend dem Höhenmesser,
sinkt das Flugzeug tatsächlich, während der Höhenmesser scheinbar eine
stets gleiche Höhe anzeigt.
... zurück zum Seitenanfang
Hat man den rechtweisenden (wahren) Kurs und will den falschen
(mißweisenden) Kurs ermitteln, so muß man die Variation mit umgekehrten
Vorzeichen addieren.
Bsp.: rwK = 49°; Mißweisung 2°W (= –2°): mwK = 51°
Will man aus dem falschen (mißweisenden) Kurs den rechtweisenden
(wahren) Kurs ermitteln, so muß man die Variation mit dem richtigen
Vorzeichen addieren.
Bsp.: mwK = 49°; Mißweisung 2°W (= –2°): rwK = 47°
Bsp.: Ein Luftfahrzeugführer erhält ein QDM von 320°. Bei einer
Mißweisung (VAR) von 12° W beträgt das QTE? Das QDR ergibt sich
aus dem QDM ± 180°
320° – 180° = 140° (QDR)
Um vom QDR (falschen) zum QTE (wahren) zu kommen muß man also das wahre Vorzeichen
benutzen.
140° – 12 ° = 128° (QTE)
Queen
Diana
Möchte
gleich (=)
Marys
Hut
und (+)
Richards
Batschkapp
Mit der Formel und ihren Ableitungen (RB = QDM – MH bzw. MH = QDM – RB)
kann man zahlreiche Aufgaben der theoretischen Prüfung rechnerisch lösen.
Zur Erläuterung:
Der Magnetkompaß zeigt den Winkel zwischen der
Flugzeuglängsachse und Kompaßnord an.
QDM ist der mißweisende Kurs zur Station. QDM gibt also
den Kurs an, den das Flugzeug zur Station fliegen müßte.
RB (Relative Bearing) ist der vom Radiokompaß angezeigte
Winkel zwischen aktuell geflogenen mißweisenden Kurs (mwK) und dem
mißweisenden Kurs zur Station (QDM)
MH ist der missweisende Steuerkurs (mwSK). Er enthält
die Korrekturen zur Missweisung (VAR) und zum Luvwinkel (WCA).
Eselsbrücke:
Steuerkurs hat immer Wind. Wenn von
Steuerkurs die Rede ist, ist immer die Windkorrektur bereits
enthalten. Das gilt also für die Kurse rechtweisender Steuerkurs,
mißweisender Steuerkurs und Kompaßsteuerkurs.
Man erhält den MH, indem man die Variation vom rechtweisenden
Kurs subtrahiert (mit dem entgegengesetzten Vorzeichen addiert).
Es gilt:
TC-VAR=MC
MC+WCA=MH
Aus einem gegebenem Kompaßsteuerkurs (CH=Compass Heading) ist
nur die Deviation (DEV) zu entfernen (mit gleichem Vorzeichen
addieren), um zum MH zu kommen.
Ein
Steuerkurs bzw.
Heading berücksichtig bereits
den
Wind
Ein
mißweisder Kurs bzw.
magnetic Kurs berücksichtig
bereits die
Variation
Ein
Kompaßkurs bzw.
CompassCourse berücksichtigt
bereits die
Deviation
- Name Deutsch (Abkürzung Deutsch)
- Name Englisch (Abkürzung Englisch)
- Enthält
- Erklärung
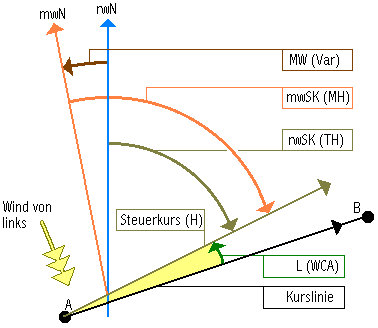
|
Abbildung |
- Rechtweisender Kurs (rwK)
- True Course (TC)
- Enthält: -
- Wird der Karte entnommen und gibt
den Winkel zwischen der Kurslinie und
rechtweisend Nord
|
 |
- Mißweisender Kurs (mwK)
- Magnetic Course (MC)
- Enthält: Variation (s. Anm. unten)
- Ergibt sich, wenn man zum
rechtweisenden Kurs die Mißweisung
berücksichtigt.
MC = TC – Var
Beispiel: TC = 70°, Variation 10°W
MC = 70° - (-10°) = 80°
westliche Mißweisung ist negativ
(der Winkel ist nach links geöffnet),
östliche positiv.Wird der Karte
entnommen und gibt den Winkel
zwischen der Kurslinie und
rechtweisend Nord
|
 |
- Kurs über Grund (KüG)
- Track (T)
- Enthält: -
- Ist ein auf den Erdboden
projizierter Kurs, den das Flugzeug
tatsächlich fliegt, wenn der Pilot
den Wind nicht berücksichtigt.
Herrscht kein Wind oder nur Rücken-
bzw. Gegenwind, so sind KüG und
rwK gleich.
|
 |
- Steuerkurs (SK)
- Heading (H)
- Enthält: Wind
- Ausrichtung der Flugzeuglängsachse,
also der Kurs, den der Flugzeugführer
steuert (um den Windeinfluß zu
neutralisieren). Der von der Windrichtung
und –geschwindigkeit abhängige
Winkelbetrag, um den vorgehalten
werden muß, heißt Luvwinkel (L)
bzw. Wind Correction Angle (WCA)
|
Bild wie eben
Merkregel:
Wind von links, Luvwinkel nach links;
Rechnerisch: negatives Vorzeichen
Wind von rechts, Luvwinkel nach rechts;
Rechnerisch: positives Vorzeichen
|
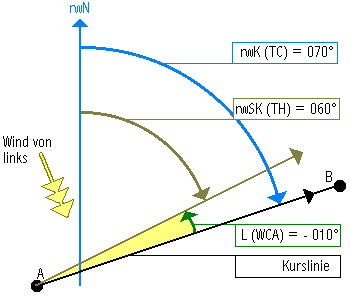
- Rechtweisender Steuerkurs (rwSK)
- True Heading (TH)
- Enthält: Wind
- Der rechtweisende Steuerkurs ergibt
sich, wenn der rechtweisende Kurs mit
einem Luvwinkel verbunden wird.
Der Windeinfluß muß genau an dieser
Stelle berücksichtig werden, da die
Gradangaben zum Höhenwind rechtweisend
erfolgen. Nur rechtweisende Größen
können miteinander verknüpft werden.
rwSK (TH) = rwK (TC) + L (WCA)
Beispiel:
RwK = 70°; L = –15° (Wind von links)
RwSK = 70° + (–15°) = 55°
|
 |
- Mißweisender Steuerkurs (mwSK)
- Magnetic Heading (MH)
- Enthält: Wind, Variation;
- Der rechtweisende Steuerkurs wird
zum mißweisenden Steuerkurs, indem
die Variation berücksichtigt wird.
|
 |
- Kompasssteuerkurs (KSK)
- Compass Heading (CH)
- Enthält: Wind, Variation, Kompaßfehler
- Zum KSK wird der mißweisende
Steuerkurs, wenn auch die
Deviation des Kompasses
berücksichtigt (subtrahiert)
wird. Ist die Deviation negativ,
so wird der Kurswinkel größer.
Bsp.: mwSK ist 70°, Deviation –7°
KSK = 70° – (–7°) = 77°
|
 |
Anmerkung: Variation = Deklination = (Orts-)Mißweisung. Die Variation
ist die Differenz zwischen Geographisch Nord und Magnetisch Nord.
Westliche Variation ist negativ (denn sie wird in einer Zeichnung
nach links – gegen den Uhrzeigersinn – abgetragen), östliche Variation
ist positiv. Die Variation wird der ICAO-Karte entnommen. Bei den in
Funknavigationskarten angegebenen Kursen ist die Variation bereits
berücksichtigt.
... zurück zum Seitenanfang
Hilft bei der Entscheidung, wie der Kurs zu wählen ist, wenn die Flugkontrolle ein Soll-QDM
anordnet.
Beispiele:
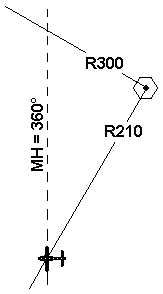
Flugkontrolle ordnet an: "Intercept 300" (bedeutet
"Nähern Sie sich dem Radial 300 an und folgen
Sie dem Radial"). Pilot stellt fest, daß er sich
derzeit auf Radial 210 befindet. Er will/soll
von der Station wegfliegen (Radial!), ist also
outbound. Da er weniger "hört" (nämlich 210), muß
er hier mehr steuern (outbound: hear less, stear more),
also das Soll-Radial + 60°. Das Intercepting Heading
ist also 360°.
|
|
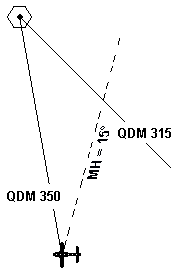
Flugkontrolle ordnet an: "Intercept QDM 315"
(bedeutet "Nähern Sie sich dem QDM 315 an und folgen
Sie dem QDM"). Pilot stellt fest, daß er sich derzeit
auf dem QDM 350 befindet. Er ist auf dem Weg zur Station
(QDM wurde angewiesen!), also inbound. Da er mehr "hört"
(nämlich 350), muß er auch mehr steuern (here more, stear more),
also das Soll-QDM + 60° (Radiale oder QDM werden möglichst
mit 60° angeschnitten). Das Intercepting-Heading ist also
(315° + 60° =) 15°.
|
|
... zurück zum Seitenanfang
In Deutsch gibt es nur das Wort Höhe. Englisch kennt folgende Begriffe
| Elevation |
Höhe des Platzes über NN (Meeresspiegel) |
| Height |
Höhe über dem Erdboden oder über dem Platz (QFE-Einstellung ergibt diesen Wert) |
| Altitude |
Höhe über NN (wenn QNH eingestellt ist) |
... zurück zum Seitenanfang
Daten, die der zuständigen FVK-Stelle (etwa Frankfurt Radar,
Berlin Radar oder Nürnberg Information – Frequenz jeweils
in der ICAO-Karte) vor Einflug in den Luftraum C unterhalb
Flugfläche 100 unaufgefordert übermittelt werden müssen:
| |
Beispiel |
| Luftfahrzeugkennung |
Delta - Echo Kilo Charlie Echo |
| Luftfahrzeugmuster |
Cessna eins sieben zwo |
| Position |
5 NM südöstlich Leipzig |
| Flugstrecke |
VFR nach Paderborn |
| Flughöhe oder Flugfläche |
In 4000 (MSL) |
| Wunsch |
Erbitte Durchflug durch Lufraum C
mit Kurs drei zwo null Grad in
viertausend Fuß |
Achtung!!
Der Kontakt mit der FVK-Stelle ist mindestens fünf Minuten
vor dem beabsichtigten Einflug aufzunehmen. Liegt der
Startflugplatz unter C, so hat die Kontaktaufnahme
unverzüglich nach dem Start zu erfolgen.
Daten, die der zuständigen Flugverkehrskontroll-Stelle
(etwa Frankfurt Radar, Berlin Radar oder Nürnberg Information)
vor Einflug in den
Luftraum C oberhalb
Flugfläche 100 unaufgefordert übermittelt werden müssen:
| |
Beispiel |
| Luftfahrzeugkennung |
Delta - Echo Kilo Charlie Echo |
| Luftfahrzeugmuster |
Cessna one seven two |
| Gesdchwindigkeit |
one two zero knots |
| Position |
5 Nautical Miles southeast of Erfurt |
| Zielflugplatz |
VFR to Hamburg |
| Flugstrecke bezogen auf Funknavanlage |
going to Erfurt VOR and further
on Radial three six zero outbound |
| Flugfläche |
flight level six five |
Fällt der Funk vor Einflug in C aus, so
darf man nicht in C einfliegen. Fällt
er während des Fluges in C aus, so ist
zu unterscheiden. In C unterhalb Fl 100
muß entsprechend der Freigabe weitergeflogen
werden, es sei denn, die VMC erlauben das
nicht. In diesem Fall ist C auf dem kürzesten
Weg zu verlassen und dabei entsprechend den
VMC zu fliegen. In C oberhalb Fl 100 muß
der Luftraum C sofort verlassen werden.
Im kontrollierten Luftraum muß unter allen
Umständen die Höhe eingehalten werden, für
die eine Freigabe erteilt wurde. Notfalls
muß man nach rechts oder links ausweichen.
Achtung !!
Für den Einflug in C oberhalb FF 100 gilt:
- Der Funkverkehr ist in englisch zu führen
(Pilot muß mind. BZF I besitzen)
- Vor der Kontaktaufnahme mit der FVK-Stelle ist
zunächst mit der zuständigen Fluginformationsstelle
(FIS) Kontakt aufzunehmen, die den weiteren Sprechfunk
einer Flugverkehrskontrollstelle übergibt.
Isogonen sind Linien, die Orte gleicher Mißweisung verbinden.
Agonen sind Isogonen mit der Mißweisung 0
NDB (Non-directional-Beacon) wird vom ADF
(Automatic-Direction-Finder) empfangen.
Dieses besteht aus drei Komponenten:
Antenne (Empfangsantenne = Loop; Richtungsantenne = Sense),
Bediengerät und Anzeigegerät.
NDB strahen auf Mittel- und Langwelle aus
(international: 190 - 1750 KHz; in Deutschland 200 – 526,5 KHz)
Störfaktoren für NDB sind:
- Gewitter
- Nacht- und Dämmerungseffekt
- Fading (Anzeige schwankt. Grund: Raumwelle und Bodenwelle treffen sich)
- Küsteneffekt
- Bergeffekt
ADF ist nicht mehr gesetzlich vorgeschrieben
und kann durch GPS ersetzt werden.
Es gibt drei Arten von Anzeigegeräten:
Beim billigsten bewegt sich nur der Zeiger,
der – wie bei allen Geräten – immer in
Richtung der NDB-Station zeigt. Den Winkel
zwischen 0 (entspr. Flugzeuglängsachse) und
dem durch den Zeiger angezeigten Wert nennt
man Relative Bearing. Um den (mißweisenden)
Kurs zur Station (QDM) zu ermitteln, muß man
nach der Formel
QDM = Magnetic Heading + Relative Bearing
vorgehen
(vgl. oben).
Ein etwas höher entwickeltes ADF nennt man
Moving Dial Indicator (MDI). Bei
diesem Gerät kann die Kompaßrose gedreht
werden. Stellt man hier den mißweisenden
Kurs ein, so zeigt der Zeiger unmittelbar
den mißweisenden Kurs zur Station (QDM) an.
Beim besten ADF,
dem Radio Magnetic
Indicator (RMI), wird die Kompaßrose
automatisch nachgestellt.
Schließlich gibt es noch Kombigeräte, die
man zugleich auf ein zweites NDB oder ein
VOR einstellen kann. Die dickere oder doppelte
gezeichnete Nadel zeigt dann auf das NDB, die
dünnere auf das VOR.
In Gebieten hoher Verkehrsdichte ist die hohe
Ungenauigkeit des NDB-ADF-Systems nicht mehr
akzeptabel. Es wird daher zunehmend durch VOR
oder GPS ersetzt. Letzteres ist aber zur
Primärnavigation (noch) nicht zugelassen.
Das
VOR (
Very High Frequency –
Omnidirectional
Range) oder
UKW-Drehfunkfeuer funktioniert wie ein
Leuchtturm. Der sendet jede volle Minute ein
Blitzlicht aus. Außerdem dreht sich ein
Lichtstrahl in einem einminütigen Kreis, und
zwar im Moment des Lichtblitzes in Richtung
Norden beginnend. Ist der umlaufende Lichtstrahl
bspw. 20 Sekunden nach dem Blitz auf den
Beobachter gerichtet, so weiß dieser, daß der
Lichtstrahl in diesem Moment mit 120° auf ihn
gerichtet ist. Der Beobachter müßte also einen
Kurs von 300° einschlagen, um zur Station zu
kommen. Beim VOR wird nicht die Zeit zwischen
Lichtblitz und Umlaufstrahl, sondern die
Phasendifferenz gemessen.
Freiheitsgrade und Kreiselachsen bei den Kreiselinstrumenten
| Kreiselgerät |
Stellung der Kreiselachse |
Freiheitsgrade |
| Kurskreisel |
Horizontal |
3 |
| Künstl. Horizont |
Vertikal |
3 |
| Wendezeiger |
Horizontal |
2 |
Merke: Alle Kreiselinstrumente haben
3 Freiheitsgrade, außer dem Wendezeiger.
Alle Kreiselinstrumente haben eine horizontale
Kreiselachse außer dem Künstl. Horizont.
Beim
Tracking erfliegt man sich ein Radial
und fliegt auf diesem Radial – also mit
Berücksichtigung des Windes – zur Station.
Beim Homing fliegt man – ohne Berücksichtgung
das jeweils aktuelle QDM (entweder durch INFO
des angeflogenen Platzes angegeben oder durch
ein Gerät angezeigt). Die Fluglinie zur Station
ist dann eine Kurve, sog. Hundekurve.
Ist in der ICAO-Karte bei einem Flugplatz
die Frequenz unterstrichen, so kann man
von dessen Flugleitung ein QDM bekommen.
Alarmstufen
| Bezeichnung |
Inhalt |
Bedeutung |
| INCERFA |
Uncertain Phase |
Ungewissheitsstufe:
Wenn sich ein Flug nach 30 Min. nicht
meldet bzw. nicht angekommen ist |
| ALERFA |
Alert Phase |
Bereitschaftsstufe:
wenn die in der Ungewißheitsstufe angestellten
Versuche der Kontaktaufnahme erfolglos waren |
| DESTRESSFA |
Not-Phase |
Einsatzstufe:
Wenn feststeht, daß ein Notfall eingetreten ist. |
... zurück zum Seitenanfang
Ende des Textes (formeln.html - 14.02.22)


 Gewollte Kursstrecke ist A – B.
Gewollte Kursstrecke ist A – B. α2 = 60 * Querablage / Reststrecke
hier also: α = 60 * 5 / 50 = 6
Lösung der Aufgabe:
Um direkt das Ziel (B) anzufliegen, müßte der
Pilot also um (10° + 6° =) 16°
korrigieren.
α2 = 60 * Querablage / Reststrecke
hier also: α = 60 * 5 / 50 = 6
Lösung der Aufgabe:
Um direkt das Ziel (B) anzufliegen, müßte der
Pilot also um (10° + 6° =) 16°
korrigieren.

 Bringt zum Ausdruck, daß der Höhenmesser zu große Höhen anzeigt,
wenn man von einem Hochdruckgebiet in ein Tiefdruckgebiet fliegt,
ohne den Höhenmesser zwischendurch nachgestellt zu haben (und zwar
auf das QNH des nächstgelegenen Flugplatzes mit Verkehrskontrolle).
Man fliegt also tatsächlich niedriger, als der Höhenmesser anzeigt.
Das liegt – kurz erklärt – daran, daß eine Linie gleichen Luftdrucks,
die zwischen einem Hochdruckgebiet und einem Tiefdruckgebiet liegt,
vom Hochdruck zum Tiefdruck verlaufend sich dem Erdboden nähert. Im
Schaubild zeigt der Höhenmesser beides Mal den gleichen Höhenwert an.
Bei unveränderter Einstellung der Bezugsgröße zeigt der Höhenmesser
auf beiden Positionen des Flugzeugs die gleiche Höhe an. Hielte man
die Höhe nur nach dem Höhenmesser (IFR), prallt man in der obigen
Situation irgendwann auf dem Boden auf.
Faustformel:
Pro hPa muß man mit ca. 30 ft Höhenunterschied rechnen. Fliegt
man also bspw. mit einer Einstellung des Höhenmessers von 1020 hPa,
herrscht aber tatsächlich ein Luftdruck von 993 hPa, so zeigt der
Höhenmesser eine um (27 * 30=) 810 ft bzw.
245 m zu große Höhe an.
Bringt zum Ausdruck, daß der Höhenmesser zu große Höhen anzeigt,
wenn man von einem Hochdruckgebiet in ein Tiefdruckgebiet fliegt,
ohne den Höhenmesser zwischendurch nachgestellt zu haben (und zwar
auf das QNH des nächstgelegenen Flugplatzes mit Verkehrskontrolle).
Man fliegt also tatsächlich niedriger, als der Höhenmesser anzeigt.
Das liegt – kurz erklärt – daran, daß eine Linie gleichen Luftdrucks,
die zwischen einem Hochdruckgebiet und einem Tiefdruckgebiet liegt,
vom Hochdruck zum Tiefdruck verlaufend sich dem Erdboden nähert. Im
Schaubild zeigt der Höhenmesser beides Mal den gleichen Höhenwert an.
Bei unveränderter Einstellung der Bezugsgröße zeigt der Höhenmesser
auf beiden Positionen des Flugzeugs die gleiche Höhe an. Hielte man
die Höhe nur nach dem Höhenmesser (IFR), prallt man in der obigen
Situation irgendwann auf dem Boden auf.
Faustformel:
Pro hPa muß man mit ca. 30 ft Höhenunterschied rechnen. Fliegt
man also bspw. mit einer Einstellung des Höhenmessers von 1020 hPa,
herrscht aber tatsächlich ein Luftdruck von 993 hPa, so zeigt der
Höhenmesser eine um (27 * 30=) 810 ft bzw.
245 m zu große Höhe an.







